You can calculate the angular velocity of a body moving on a circular path using an online angular velocity calculator. Angular speed can be calculated in three different ways using this angular speed calculator, including:
- Distance between angles.
- Radial speed.
- Velocity in angular and linear directions.
Here we will discuss the angular speed formula, how to calculate it manually, and other terms related to it.
You can also determine the speed/velocity of a moving object using an online velocity calculator.
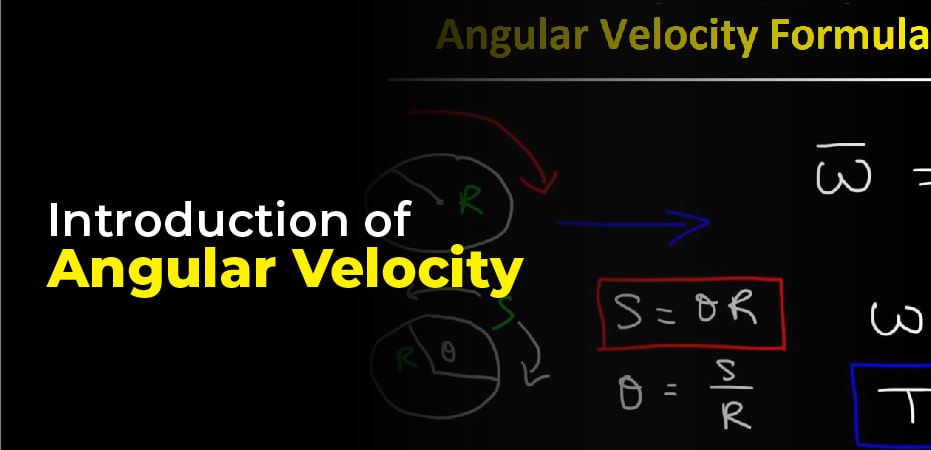
Introduction of Angular Velocity:
Angular velocity is the speed at which an object rotates or revolves in a circular path relative to another point. Angle velocity refers to the rate at which the object’s angular position changes. This is typically represented by the symbol / (ω/) /((Omega)/) and measured in /(rad/s) \ ((radian per second) \).
For instance:
The Earth completes one rotation around the sun in one day, or 360 degrees per day. Its angular velocity will be \ (ω = \frac {360°} {24h} or ω =\frac{2ᴨrad} {86400s} \).
Calculation of Angular Velocity:
In other words, angular velocity is a measure of how much angular distance an object or particle covers around something over a period of time and is measured in angle per unit time. Radians per second are the standard measurement, although degrees per second, revolutions per minute (rpm) and other units are frequently used in practice and our calculator supports most of them as output units.
The angular speed calculator can be used to calculate the angular velocity of a body traveling on a circular path. An angular speed meter can be used to calculate the speed of a Ferris wheel, a carousel, a CD-ROM or DVD, and basically anything that rotates or moves on a circular path. You can also calculate the angular momentum at the Earth’s surface and the angular speed in its orbit around the Sun with it, even if the circles are not exact. The RPM to angular velocity calculator can be used if RPM is known.
If linear velocity is calculated, the output is in metric and imperial units: m/s, ft/s, km/s, km/h, miles/s and mph. When the output is the path radius is given in meters, feet, kilometers, miles and even light years and parsecs for really large distances.
Equations of Angular Velocity:
Angular velocity vectors always run perpendicular to the plane in which an object is rotating, so finding it is straightforward using simple equations. Following is the formula for angular velocity (ω, Greek letter omega) expressed as the frequency of rotation of a body (f):
On the other hand, the second equation represents angular velocity in radians. We can obtain angular velocity from the third formula by knowing the linear velocity and radius of the circular path of an object. We can derive the linear velocity formula from a simple transformation of equation three:
ν= r. ωrad
It is valid to use these formulae for rigid bodies, but they can be approximate for non-rigid ones.
Calculation of Angular Speed – The Examples:
- Example No 1:
There are 10 revolutions per minute on a kid’s carousel. What is the angular velocity in degrees per second? Convert revolutions per minute to degrees per minute first. In terms of revolutions per minute, ten revolutions equal 3600°. We divide 3600 by 60 to get 60°/s by dividing by a minute of 60 seconds. You can also perform this calculation by using the first and second angular speed equations above: f = 60/10 = 6 seconds per rotation so ωdeg = 360 / 6 = 60°/sec and ωrad = 2 · π / 60°/s = 6.283184 / 6 = 1.0471973 radians per second.
- Example No 2:
There are 20 meters of radius on a Ferris wheel whose linear velocity is 0.5 meters per second. The angular velocity of the Ferris wheel is measured in radians per second. In this case, we use the formula ωrad = r / v = 20 / 0.5 = 0.0250 radians per second. The linear speed calculator above will confirm the calculation.

